We know that making astronomical observations of targets close to the horizon can be affected by atmospheric effects of reddening, extinction and refraction. Previous posts have addressed some of these effects, and this post asks the question: How might atmospheric refraction be measured?
Ok, so first of all, recall that because of atmospheric refraction if you look at a target star or object that is very close to the horizon, then the object will appear to be higher in the sky then it actually is in reality. It turns out that the object will appear higher by an amount determined by a formula proportional to the cotangent of the measured elevation. Can we measure this effect?
Hmm, what if we were to measure the angular separation between two objects, when they are high above the horizon, and then at a later time as both objects, one higher than the other, fall down and below the horizon. If we now measure the separation between these two objects, this second measurement should show that the separation is less because the position of the object nearest the horizon will be distorted and measured to be higher in the sky than it really is.
So, I went outside and found one convenient object, Venus, that was about 10 degrees high in the sky and would shortly deep down between the palm tree and the streetlight in the photo shown below, This photo was taken with DSLR telephoto lens set to 35mm, which gives a field of view of 24 x 36 degrees and a pixel size of 25 arc seconds. The amount of refraction is estimated to be 5 arc minutes and 14 arc minutes for 10 degree and 3 degree elevation, respectively.
 |
| Venus at 10 degrees above the horizon, after sunset, with bright streetlight (Source: Palmia Observatory) |
Now after waiting around for 30 minutes, Venus dipped down to about 3 degrees above the horizon. I took another photo of Venus and used Sky Safari Pro to determine the elevations. The cropped image below shows Venus, now just to the right of the palm tree, and the positions of two reference stars. You probably can't see the stars in this image because they are dim, between magnitude 4-6.
 |
| Venus at 3 degrees elevation, with two reference star locations (Source: Palmia Observatory) |
So, next, I measured the pixel distance between the Venus and Reference Star 1, using the first photograph and then measured again the same distance but this time using the second photograph. Maxim DL software was used to find the centroid locations of the targets, from which the distances could be calculated. See the screenshot for the case of measuring Venus' pixel location.
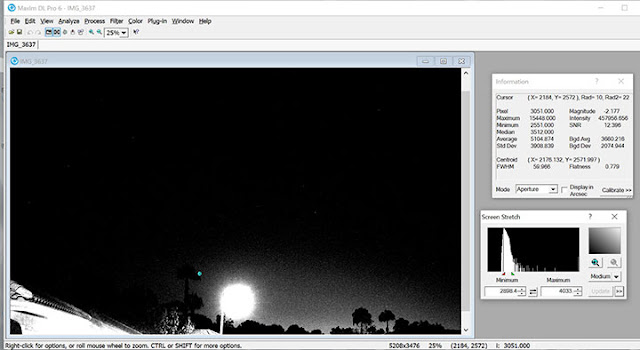 |
| Use Maxim DL on 9:07 PM and 9:42 PM images to find target centroids (Source: Palmia Observatory) |
The first distance was measured as 1743 pixels and at the later time, when Venus was just 3 degrees above the horizon, the distance was measured as 1644 pixels.
Hey, so far this is looking pretty good because the second distance is less than the first, which is just what we would expect from atmospheric refraction, which causes Venus' position to appear higher in the sky. The distance measured is shorter by (1743 - 1644) * 25" = 99 * 25" = 41 arc minutes, which is about 3 times what refraction effects estimates would predict. So what is going on?
Ok, ok, you probably see a couple of things already. First of all, the refraction effects will also distort the first measurement also, not as much as the second one because the objects were higher in the sky. I could have taken the first image a bit earlier in time, but that issue is probably not the major source of error. The other source of error is that the photo image is flat while the stars can be thought of as being on the celestial sphere. We have learned earlier when doing some astrometry and trying to fit images of star patterns to their catalog RA and Dec positions, that the errors build up very quickly for wide field of views like the 24x36 lens used here.
We can check this out by measuring the distance between another star. The second reference star was chosen to be more horizontal with respect to the first star. The measured distance between Reference Star 1 and Reference Star 2 in the two images is found to be: 2286 pixels in the first photo and 2201 pixels in the second photo. The different length here is 85 pixels and both stars are further away from the horizon.
Hmm, yeah, it seems there is just too much error in measurements due to wide field of view considerations to get any useful measurements of atmospheric refraction. We could use a narrower field of view lens, like a 300mm lens, to correct one source of error, but then the narrower field of view would have the two reference stars very close together and near the horizon, so they both would have mostly the same refraction effects.
So, how do we go about measuring atmospheric refraction? I suppose we could do something like take photos with small field of view, to get rid of the non-linear issues and then measure the rate of change of approach to the horizon, which should slow down because of refraction. Anyone have another approach in mind? I might have come out further ahead by spending more time looking at the very bright Mars, but this project was fun, even if in the end it did not result in any meaningful measurement!
Until next time,
Resident Astronomer George
If you are interested in things astronomical or in astrophysics and cosmology
Check out this blog at www.palmiaobservatory.com

No comments:
Post a Comment