Well this week we return to angular momentum and the interaction of dark matter and even consider throwing a satellite or baseball made out of dark matter and watching how it flies.
First up recall in our previous posts of August 25, where we discussed spin rates of giant gas planets and how some additional torque, in this case magnetic torque, was required to account for the present day planet spin rate. This post used conservation of momentum to explain how an external torque was required to explain the present day spin rates. Then in a previous post of August 20 we considered Kepler's Law of planetary motion and how the orbit radius and period were related, again using angular momentum.
Today we consider how dark matter, so necessary to explain the orbital motion in galaxies and large scale structure formation, is constrained by the conservation of angular momentum, and cannot easily collapse into stars or other objects. This is illustrated in the image below which shows the expected dark matter halo around a much smaller, yet brighter, spiral galaxy.
So what is going on here? As you already know, and as Ethan Siegel explains in his "It Starts with a Bang" blog, the dark matter, since it is assumed to mostly interact with normal matter only gravitationally, cannot shed it angular momentum and it resides in the halo, while the ordinary matter can shed angular momentum and collapse into stars and galaxies. The normal matter follows the gravity well created by the dark matter but otherwise does not interact with it.
 |
| Dark Matter halo extends much wider than visible galaxy (Source: Ethan Siegel, "It starts with a bang", Aug 24) |
Ethan Siegel's blog post goes on to explain that there is probably not much dark matter in ordinary stars or in black holes either. It is not because the dark matter is not gravitationally affected but again because it can't easily lose its angular momentum and fall into the star or black hole. It would tend to just sort of orbit around it. Also when we talk about angular momentum being lost, it does not mean that it disappears entirely, but is really just transferred to other objects as the matter falls into forming a star or planet formation. It is very interesting to note that even though there is something like 5x as much dark matter in the universe as there is normal ordinary matter, but when you look at any given volume of the universe, such as the volume of space around us in our solar system, then the amount of dark matter contained there is only about 1/2 ton of dark matter for every billion tons of ordinary matter. Thanks for that illuminating discussion, Ethan!
We should mention here though that in previous posts of April 14 and August 1, 2019, we also mentioned the idea of dark stars, which have a great deal of dark matter. This idea of dark stars comes from Katherine Freese, U of Mich., and associates who argue that when the universe was young and very dense it could have been possible for dark starts, composed of a lot of dark matter, could have formed. Dark matter particles can interact and annihilate when they get close enough and the energy released is supposed to be such that the collapsing cloud does not get dense enough for fusion to start, but the mass of the protostar can get say thousands to millions of times more massive than the sun. She argues that these stars could have grown very large and could have been the seeds from which supermassive black holes were formed. Neat, but I still don't understand how the dark matter lost its angular momentum.
Anyway, Ethan goes on to discuss what might happen if we could have a baseball made out of dark matter and how it might behave if we pitched the ball up in the air. Hmm, well, first of all we have to "imagine" that the dark matter would stay in the shape of the baseball and would not just slowly disperse, but let's give him this assumption. Secondly, we have to assume that we could somehow "throw" the baseball given that the dark matter would not respond to us since we made of ordinary electrons and such. But the idea is what would the trajectory be for this dark matter baseball?
In Ethan's #100 blog posting, he describes this imaginary scenario of throwing a dark matter baseball and following its trajectory. The baseball would not be affected by normal air molecules or other normal electromagnetic forces and would only respond to the gravitational field of the Earth. So it would "fly" on a normal parabolic trajectory until it comes back to the Earth's surface. Then what happens? Nothing, it just passes right through the Earth and continues on its gravitationally driven path right down to the center of the Earth, as shown below.
 |
| What happens if you throw a baseball made of dark matter? (Source: Ethan Siegel, "#100: It starts with a bang", 8/7/15) |
Wow, so that is pretty neat! What happens as the baseball continues on this journey? Well the illustration above is not quite representative of what the trajectory would actually look like. The illustration just shows what would happen if all of the Earth's mass were concentrated at one point, at its center, but that is just an approximation.
You might have remembered seeing the original "Journey to the center of the Earth" 1959 movie staring James Mason, Pat Boone (and others), like I did when I was a youngster. I still remember one of the most vivid scenes was when the group is trying to escape in a raft and a giant lizard is after them and the beautiful character portrayed by Diane Baker, trips and falls. When Pat Boone's character rushes back to save her, I remember almost screaming, "Don't go back, leave her there; don't get eaten by the lizard." Well, sadly, I was a little too young to appreciate the attraction for saving the beautiful damsel in distress and his love interest!
But continuing with the movie, when the explorers got to the center of the Earth, forget all about what we know now about how it is probably a very hot solid ball of iron, they were being pulled in all different directions. It seemed the movie explained this with magnetic fields or something, I don't really remember, but the reality would be that the gravitational field would have mostly cancelled out and the explorers would have been weightless. Well, the baseball in our imagination would experience the same effect, and it would not care that the core was actually solid iron or anything else. It would not feel any gravitational attraction and so would just speed on by, except now its forward motion would be retarded by the gravitational field that it would begin to experience.
So, that is really what would happen and the baseball would continue falling and accelerating towards the center of the Earth and would reach its maximum velocity just as it passed the center and then then would continue moving through the interior of the Earth until it worked its way up the gravity well to the other side of the Earth. So, it would not turn around just after passing the center of the Earth, but would continue on to the opposite side and surface of the Earth.
But how far above the opposite side of the Earth would the baseball go and what would happened next? Hmm, this type of problem is exactly the problem that I can use as an example of gravity calculations using Python. Now I had done a lot of previous software coding in Basic, Fortran and C, but as every aspiring astronomer wannabe now, the language of choice is Python. So, I put together the example of a dark matter baseball and used Python to solve the set of ordinary differential equations governing its trajectory.
The graph below shows the radial position and velocity of a dark matter baseball if it were just dropped and allowed to fall under the influence of gravity. The blue curve shows the ball starting at the Earth's surface, 6356 meters above the center of the Earth. As the ball falls, it accelerates and reaches a maximum velocity of about 8 km/second at the center and then slowly decelerates until it reaches the other side and surface with velocity of again, zero. What happens next? Well, no other forces affect the dark matter baseball so it just falls down again and keeps up this strange type of orbit around the center of the Earth's gravitational field.
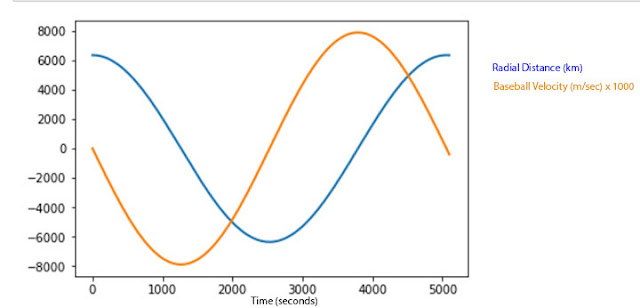 |
| Dropped Dark Matter Baseball just oscillates through the center of the Earth (Source: Palmia Observatory) |
Ok, so what would happen if we actually pitched the dark matter baseball? Hmm, let's pretend that we pitch it really fast, as say 3 km/sec, horizontally, and 3 km/sec, vertically, just so the distances show up on a graph of the whole Earth. This condition is shown in the graph below. The Earth's surface is represented by the orange circle and the trajectory of the baseball is shown in blue. This plot is generated in Python by solving the coupled ordinary differential equations for the situation. Note that the baseball comes right back up to the same location from which it was pitched from, some 5000 seconds earlier. This approximate 83 minute round trip journey is essentially the same as would be required by a satellite launch in a very low Earth orbit.
 |
| Launch a DM baseball (blue) and it orbits around the center of the Earth (Source: Palmia Observatory) |
Ok, so that was a pretty neat little example with which to write a little Python code. If you are interested in what the code to calculate these orbits looks like, check out the code printout below. There are probably many ways to improve on the code layout and structure, but at least I found my way through to the end of writing and debugging (mostly debugging) one of my first in a long time Python coding examples.
 |
| Python coding to solve gravitational orbit equations for dark matter baseball (Source: Palmia Observatory) |
Until next time,
Resident Astronomer George
Be sure to check out over 300 other blog posts on similar topics
If you are interested in things astronomical or in astrophysics and cosmology
Check out this blog at www.palmiaobservatory.com

Excerpt:
ReplyDeleteGravity is understood to be an attraction between objects. The pull of dark matter might be thought of as a ‘stickiness’. Particles and objects within a cloud or halo dominated by dark matter find themselves bound, over distance, to each other, as long as the objects remain within the dark matter cloud. If that is the case, then dark matter may not be a physical particle, instead is a kind of ambiance that induces a certain relationship amid particles and larger bodies. When momentum comes into play that ambiance is shook-up.
Again, the activity or influence of dark matter is so integrated into common activities that we do not notice its effect.
Great post, and great website. Thanks for the information! telescope to see planets and galaxies
ReplyDeleteI think this is an informative post and it is very beneficial and knowledgeable. Therefore, I would like to thank you for the endeavors that you have made in writing this article. All the content is absolutely well-researched. Thanks... dark web sites
ReplyDeleteYour kid may not be explicitly searching for its substance, rather simply perusing for interest.deep web sites
ReplyDeleteWow! Such an amazing and helpful post this is. I really really love it. It's so good and so awesome. I am just amazed. I hope that you continue to do your work like this in the future also Camera BF Deals
ReplyDeleteI read that Post and got it fine and informative. Offers
ReplyDeleteWe are really grateful for your blog post. You will find a lot of approaches after visiting your post. I was exactly searching for. Thanks for such post and please keep it up. Great work. dark web links
ReplyDeleteHello I am so delighted I located your blog, I really located you by mistake, while I was watching on google for something else, Anyways I am here now and could just like to say thank for a tremendous post and a all round entertaining website. Please do keep up the great work. dark web links
ReplyDeleteNice to read your article! I am looking forward to sharing your adventures and experiences. hydra onion
ReplyDeleteI went over this website and I believe you have a lot of wonderful information, saved to my bookmarks гидра не работает
ReplyDeletethank you for your interesting infomation. dark web sites
ReplyDeleteI think this is a really good article. You make this information interesting and engaging. You give readers a lot to think about and I appreciate that kind of writing. dark web links
ReplyDelete