Clouds and no Starlinks; Beta equilibrium and neutron stars; Studying physics at the Casinno de Urca? It is hard to fall into the sun; EHT Black Hole shadow with Fourier analysis at the 157th NAS annual meeting

Greetings from Palmia Observatory

Well, it was a clear night and we hoped to glimpse a string of pearls view of the recent Starlink satellite launch, but
the clouds actually were in the way.  The night sky around Venus and the Moon and Arcturus and Sirius was indeed very clear, but it turned out the clouds were hidden in the dark sky toward Polaris.  The predicted pass of the Starlink satellites, as described in the last blog post, was low on the horizon, starting in the North and moving to the Northeast.  So, even though the clouds could not easily be seen in the northern sky, you can see that they were very thick in this  image.  But we should be able to try again tonight, beginning at about 8:42 PM in southern California.

Clouds blocked any view of the Starlinks in this DSLR, 80 mm, 10 second exposure (Source: Palmia Observatory)

Ok, we were disappointed in not seeing the string of pearls, but we have some more physics activity and comments.  First, I had a chance to sit in on a masters thesis defense at CSULB and even though the presentation was well done it was mostly over my head, but I learned one key point about neutrinos and neutron stars.

The student showed the equations for converting neutrons to protons and vice versa and how equilibrium conditions between the two is a function of temperature, pressure and other conditions.  Rather than show any of the student's work, we can more easily see the Beta equilibrium equations from this paper by Alford and Harris, "Beta Equilibrium in Neutron Star Mergers", for example.

Beta equilibrium equations (Source: Alford & Harris, arXiV: 1803.00662)

Previously, when I saw these equations I thought that the equilibrium condition would be when the direction of the arrow was reversed and the reaction just moved in the opposite direction.  But, this assumes that there is a ready supply of neutrinos (both regular and anti) to make the reaction go.  But this is not necessary in that if we just consider the two equations as a system then neutrons can decay to protons and then protons, in the second equation can be converted back to neutrons, without the need for a supply of neutrinos to make the reaction go.  So, this was a neat realization for me, because as we know that the exiting flux of neutrinos helps cool the star and the density of neutrinos might not be high enough to make the reverse direction occur.  Other conditions for beta equilibrium fix the stability of neutrons in a neutron star.

This paper described these reactions as Urca processes, but what does this mean.  Well, we learn later, in a Wikipedia reference the story behind why these processes are called Urca processes.  It turns out Gamow and Schenberg were visiting a casino in Rio de Janeiro called "Cassino da Urca" when they developed this process and named it based on the analogy between energy losses and how energy flies out from a star in the form of neutrinos and how quickly money flies out of the pockets of attendees at the casino.  Hmm, see, just because some physicist wannabe seems to be gambling and drinking away and lollygagging about does not mean that some creative thinking and discovery is not also going on!

The Urca process and analogy as told by Gamow at the Cassino de Urca (Source: Wikipedia)

Another "aha moment" occurred after considering the case of how gas clouds during the early age of the universe can shed their angular momentum and continue collapsing to form galaxies and stars.  It turns out that losing angular momentum is also a problem for satellites that want to get close to the sun.  Why?  Well, the Earth moves around the sun in its orbit at about 67,000 mph.  If a satellite wants to fall toward the sun, it needs to reduce its orbital velocity.  But it must lose its orbital velocity in the right way because if it just starts reducing its orbital velocity it will just fall back onto the Earth.  So a satellite in Earth orbit, say at 17,000 mph, just can't reduce its velocity, but first must increase it velocity to something like 25,000 mph so that it can leave Earth orbit.  But even then it must follow a well defined plan to reduce orbital velocity and this takes a lot of fuel.  Also for orbits closer to the Sun, like Mercury for example, its orbital velocity is about 107,000 mph.  So many space probes have left Earth gravitation influence, but to leave the gravitation influence of the sun and actually leave the solar system, like the Voyager missions, requires so much fuel it is not easy to do.

At the same time, much fuel is needed to cause the space probe to fall toward the sun.  This problem is well illustrated by the recently launched Parker Solar Probe, which is still on a complicated flight path that brings it closer and closer to the sun.  It relies on gravitational assists from Venus to slow itself down and approach the sun.  The gravitational assists for other space probes is often used to gain extra velocity to travel to the outer planets of the solar system.  Anyway here you can see how the Parker Solar Probe makes its journey to the sun.

Parker Solar Probe -- Journey to the Sun (Source: www.parkerspaceprobe.jhuapl.edu)

In the screenshot below you can see the wildly eccentric orbit of the Parker probe as it gets closer and closer to the sun.  So you can see that the probe doesn't spend too much time really close to the sun.  Initially, I though the probe was going to be in a close orbit like Mercury, but we see not that this is definitely not the case, even when the orbit does take it closer to the sun than Mercury.

Eccentric Orbit of the Parker Solar Probe -- Journey to the Sun (Source: www.parkerspaceprobe.jhuapl.edu)

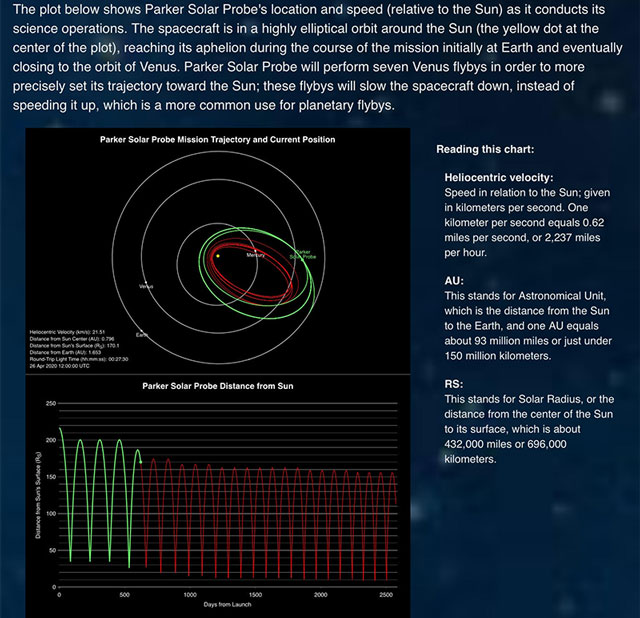The final topic for now covers one of the technical sessions of the just concluded 157th National Academy of Science (NAS) annual meeting.  This meeting too was conducted as a virtual meeting online.  I found this one session on "Discovering and Imaging Black Holes" particularly interesting.  Here, Feryal Ozel, U. of Arizona, begins her presentation on "Black Hole Shadow in M87."

The Black Hole Shadow in M87 (Source: Feryal Ozel, 157th NAS Annual Meeting)

My intention here is to emphasize my understanding of how Fourier analysis is used in modeling the Event Horizon Telescope (EHT) data and producing the image of the black hole shadow.  Many of you will have worked with Fourier analysis and transforms.  For me, it was in working electronic signal analysis and using Fourier transforms in going from time domain analysis to frequency domain analysis.  In the screenshot below we see how analysis of the individual baselines of telescopes in the EHT can be perform in the Fourier domain and how a pattern begins to emerge from this analysis.  Yes, we can start to see some periodicity in the data.

Looking at the baseline and interferometry data with Fourier (Source: Feryal Ozel, 157th NAS Annual Meeting)

If the EHT data is modeled by just a simple circle, we see after adjusting the diameter of the circle, that the Fourier analysis of the circular image, shown in green, begins to look a lot like the EHT data.

Fourier analysis of circular image to EHT data (Source: Feryal Ozel, 157th NAS Annual Meeting)

Next, see what happens when a ring, instead of just a circular image, is used in the Fourier analysis.  Here you can see that the simulated ring image now begins to fit the actual EHT Fourier pattern much better.  Professor Ozel goes through several iterations like this to show how modeling and comparison to the data begins to identify what type of structural pattern is contained in the EHT data.

Simulated modeling with a ring structure fits the data better (Source: Feryal Ozel, 157th NAS Annual Meeting)

Finally, after adding other modeling techniques and using a pixel based approach, that does not include any initial bias as to what structure is contained within the data, we get much closer to the final image of the black hole shadow.

So, what do we see in this image?  First note that it is not symmetric in that the bottom is much brighter and wider than the top.  This difference is attributed to the swirling gas that surrounds and follows in toward the black hole and in this case the bottom view is brighter because the gas is seen approaching us and is therefore brighter and the upper portion is flowing away from us and is then Doppler shifted to a dimmer view.  The central portion of the image is the shadow of the black hole and no photons from that region reach us.

Getting closer to the final model of the Black Hole Shadow in M87 (Source: Feryal Ozel, 157th NAS Annual Meeting)

Professor Ozel goes on to explain how using general relativity we can compute and identify the mass of the black hole with the diameter of the event horizon here seen as the shadow.  The measured size of the shad is 42 micro-arcseconds, which corresponds to a mass of the black hole at about 6.5 billion solar masses.  Hmm, pretty big, especially compared to the black hole at the center of the Milky Way is something like 4 million solar masses.

Anyway, that was a very interesting presentation.  It is still probably online if you have not already had a chance to see it and other presentations.  Here is the summary slide.  Thanks for the presentation, Professor Ozel!

The Black Hole Shadow in M87 and measured data (Source: Feryal Ozel, 157th NAS Annual Meeting)

Until next time, here from our burrow, stay sane, stay safe,

Resident Astronomer George

Be sure to check out over 400 other blog posts on similar topics

If you are interested in things astronomical or in astrophysics and cosmology

Check out this blog at www.palmiaobservatory.com