Greetings from Palmia Observatory
Well, we didn't get any nighttime observing done this week and we were mostly preoccupied with wondering about the effectiveness of the 2nd COVID-19 vaccine shot.
This MedPageToday provided one piece of data indicating the timeline of improving effectiveness following the 2nd shot. We see there is at least one data point saying the effectiveness goes up from 46% to 92% just 7 days after receiving the 2nd shot. So, does this mean that after 7 days we are going to see a whole lot of folks, not so worried much more about contacting the disease themselves, but who now feel freer to travel and go about? Many people that I bumped into said, yes, the first thing they were going to do was to get airline tickets and fly to see their kids or grandkids. In the meantime, we are still waiting to get more data about the best policy going forward.
 |
| Effectiveness timeline for 2nd vaccine shot (Source: MedPageToday.com) |
In previous posts we discussed various online lectures and books that go into all of the details of viruses, including introduction to virology for medical students, but if you don't have that much interest to spend a lot of time on those topics, then check out this very short video on COVID-19 vaccines presented by Ninja Nerd Lectures. This lecture covers three aspects of the new vaccines starting with (1) The FDA emergency approval process, (2) How three of the vaccines work, and (3) Reviewing how the test trials are used to calculate the statistical effectiveness of the vaccines.
 |
| Great introduction to vaccines and FDA approval process (Source: Ninja Nerd Lectures) |
The lecture presents a high level description of how the vaccines work. The Pfizer and Moderna vaccines are mRNA vaccines that rely on the body's own cellular ribosome machinery to translate the mRNA into the spike protein associated with the SARS-CoV-2 virus, while the Astrazeneca vaccine uses a harmless adenovirus to to get DNA into the nucleus, from where the nuclear machinery makes the proteins that enable the production of the viral spike protein.
 |
| Explanation of what the vaccines do (Source: Ninja Nerd Lectures) |
So, regardless of how the spike protein gets manufactured inside the cells, the immune system learns to spot the spike protein and begins to learn how to begin a defense against cells that make the protein. The effectiveness of the vaccine then can be measured by computing the statistics of the trial groups. When the statistics, between the trial group that received the vaccine is compared to the trial group that received a placebo, are compared then the effectiveness of the vaccine can be determined. For example, of the 15,000 people receiving the placebo, 182 people were found to have contracted the disease, while of the 15,000 people who received the actual vaccine, only 11 people were found to have contracted the disease. With these small numbers it is still statistically valid to establish the effectiveness of he vaccines.
 |
| Calculating vaccine effectiveness using trials data (Source: Ninja Nerd Lectures) |
If you want you can check out the lecture series yourself at: https://www.youtube.com/watch?v=35Idb_lCU4o&feature=youtu.be.
In the meantime, I was curious about how much mRNA is injected for each dose. It turns out that the Pfizer vaccine is said to contain 30 micrograms of mRNA plus other lipid nanoparticles and other compounds. Let's take a look at how many molecules are in the equivalent 30 micrograms of mRNA which we can calculate by making a lot of assumptions.
What we know is that the spike protein is composed of a chain of 234 amino acids and the mRNA to manufacture this protein must be at least 3 times longer to account for how RNA is translated into proteins. So, using this starting point and some other assumptions, the Python code segment shown below calculates the number of mRNA molecules injected. The assumptions include an average estimate for the molecular weight for the average amino acid.
Compare this number (2.1E+14) with the number of cells in the human body, thought to be something like 30 trillion, or 3E+13. So, if the assumptions made in this example are correct there are more mRNA molecules in the injection then the number of human cells. If these calculated estimates, with all of their associated assumptions, is correct then the ratio of mRNA to cells is 7.3 to 1. Additionally, each mRNA molecule can make more than than one spike protein. Some references say that a mRNA molecule can make upwards of 900 proteins before it becomes degraded and is destroyed by other cellular machinery.
 |
| Trying to estimate the number of mRNA molecules in vaccine dose (Source: Palmia Observatory) |
We can do another little bit of Python practice and calculate the Poisson probability for the allocation of mRNA per human cell. We know based on the previously calculated estimates, one dose contains about 7.3 times the number of mRNA molecules than cells. Typically in random distributions like this the average will bounce around a bit with some cells getting no mRNA and other cells getting more than the average. Let's use a little Python coding to estimate the probabilities for this Poisson process.
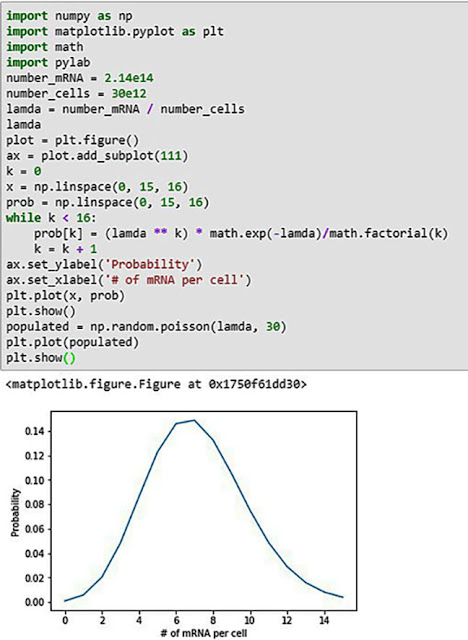 |
| Poisson distribution of mRNA among the 30 trillion cells (Source: Palmia Observatory) |
So, you can see from this chart of the probability estimates that on average there will be 7.3 mRNA per cell, but that there will be about 0.08% of cells that just by chance get no mRNA molecules.
How accurate you ask are these estimates? A lot of assumptions are made here and the lesson learned is mostly just that we can estimate the number of molecules involved by making these assumptions. Maybe if we find actual projected estimates in the literature, we can review that then. At least, it was good practice to jolt the old memory cells to remember Python coding.
Ok, enough of speculating about the number of mRNA molecules, let's follow up and do some calculations on another topic brought to us by Science Nerd & OCA, Scott, who followed some discussion of a group at the University of Bristol, who are trying to develop new energy storage batteries based on Tritium and diamonds. Hmm, for some reason this does not sound very cost effective, but in lieu of diving more into that particular claim let's review how Tritium itself might enter into the energy storage business. Anyway, in this screenshot you can see a prototype product that was built to test the feasibility of these devices. There are many applications for long-life, low power storage devices, but I have not looked into the status of any of these applications and available products. There will always be the precaution that the battery is radioactive and precautions have to be taken.
 |
| Tritium batteries for very low power, long life applications (Source: City Labs) |
Remember that Tritium is just the heavy version of hydrogen and has two neutrons in the nucleus rather than one or none in the more common isotopes of hydrogen. Tritium is unstable and decays by emitting an electron, turning into Helium 3. The Helium 3 nucleus will also be looking for one more electron. The antineutrino just escapes and does not pose any risk. The half life of the reaction is 12.3 years. The emitting electron, called a beta particle, has a kinetic energy of 5,700 electron volts. For Carbon-14 the radioactive decay releases a beta electron and the carbon is converted into normal stable nitrogen.
 |
| Decay of Tritium to Helium 3 and beta electron (Photo Source: physics.utah.edu) |
Other radioactive materials have also been considered for energy storage applications including Carbon-14, with a half life of 5730 years and a decay energy of 156,000 electron volts. Again, because the emitted electron is called a beta particle, the science around making batteries from these materials are called betavoltaic technology. The batteries intercept the emitted beta particle and convert some of the energy into electricity as outline below.
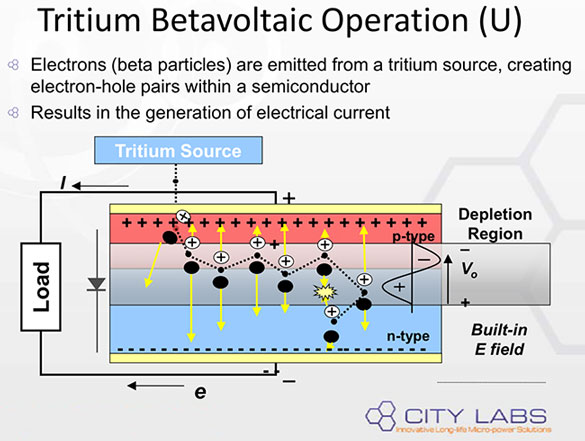 |
| Capturing Tritium beta decay energy as electricity (Source: City Labs) |
So, the major advantage of a battery of this kind is the long life of producing power, which could be as long as 12.3 years for Tritium or 5730 years for Carbon-14. The practical problem of course is the low power output of such devices. Let's do an estimate of the maximum power available from a kilogram of either tritium or Carbon-14. Again, we can use Python as a practice exercise in coding up the calculations. In the screenshot below, we see that 1 kg of Carbon 14 releases an average of 2.97 watts for 5730 years and 1 kg of Tritium would release 236 watts for 12.3 years. So, if you want a storage of energy that keeps going for many years, this technology might work ok, but if you want a lot of power in the here and now, it is not very effective.
 |
| Average power from radioactive decay of 1 kilogram or T or C14 (Source: Palmia Observatory) |
So, it is not clear that this technology is going to have any impact on the current need for high power energy storage, but the theoretical energy storage capability for Tritium is very good. For example, the standard energy density for lithium-ion batteries is taken to be about 1 million joules per kilogram. The 236 watts from 1 kg of Tritium can run for 12.3 years, over which time the total amount of energy released could be 236 * 31,536,000 = 7.4 billion joules over just one year. Looking at this amount of energy we see that a 1-kg of Tritium battery would be able to provide 1 million joules in just a little bit longer than 1 hour and keep doing that for many years.
Of course all of these estimates are purely theoretical possibilities. It is not clear to me how the 5700 eV energy per decay of a tritium atom can ever be completely recovered at high efficiency. Most semiconductors that can generate electricity with the beta electron have band gaps in the several eV, so how is most of the available energy recovered? Do you arrange several thousand semiconductor diodes in parallel so that each one accepts just a fraction of the decay energy, but that all together they collect most of the decay energy? I don't know and we will have to wait for more information.
Until next time, here from our burrow, stay safe, as we recover more of our freedom,

No comments:
Post a Comment