General Relativity at 100 Celebration in Pasadena, Eddington's measurement of the bending of light during an eclipse, Collecting images of Jupiter's moons and measuring locations to plot orbits

Greetings from Palmia Observatory

Well, this week has been a busy one with collecting images of Jupiter's moons as part of my interest in collecting real data in order to calculate and predict the orbits of the moons and more generally, orbits of other planets or asteroids.  There are plenty of data sources on the Internet and even apps for your phone which can identify the orbital and observational parameters, but
my interest is in being able to predict orbits based on observations that the amateur can make today.

During the recent General Relativity at 100 Celebration, I was quite impressed by one of the speakers, Collin Harris, who is a sociologist of science.  Last post I mentioned him and just started reading his book, "The Golem", where he describes some of key scientific discoveries and the sociology of the culture in which the scientists operated.  The one experiment described there, that is especially relevant to the observations that I will shortly describe here, was the Eddington observation and verification of the gravitational bending of light.  Eddington used the sun as observed during an eclipse to verify that the observed positions of stars shifted in position due to the sun's gravity.  A review of the measurements shows that the determination was not quite as clear cut as we were led to believe in that some of the data was excluded in order to agree with Einstein's prediction.  It wasn't dishonesty, just a value judgement of what data points were outliers and shouldn't have been included.  Again, an example of what the scientific culture expects and allows at the time the observations were made.

As amateur astronomers, we should ask how this deflection of light observation could be made?  We know that during the eclipse it is possible to see the background of stars near the sun and to measure their apparent position.  But how do you know how much the position has shifted?  You need to know the apparent position of the stars when the sun is not present.  How do you do this?  What Eddington had to do was to take a photo of the stars when the sun was not there and compare the positions of the stars when the sun was there.  Since the stars are really only visible at night, he did this by taking images of the stars at either several months earlier or later than the date of the eclipse.  Wow!  Just imagine all the things that could change during the months between these observations?  The telescope could have sagged or the temperature changes affected the scope and maybe changed its focal length or atmospheric changes or many other effects.  To ensure that the comparison between these two different images was going to be relied on it is necessary to take all of these other details into account.

So my attempt at making astronomical observations in order to verify some aspect of astronomy is not going to be as complicated as Eddingtons's, but attention to detail is still needed.  So as I mentioned earlier, I've been gathering images of Jupiter and moons in order to measure and predict the moon's orbits.  The physics of how to do this has been known for several hundred years now, but my interest is in duplicating the measurements myself.  Another OCA member, Still a Teenager, Sydney, just completed gathering 1/2 of the needed observations of Jupiter's moons to make an estimate of the speed of light.  Her project is to repeat Roemer's experimental determination of the speed of light conducted in 1676.  This process and many other projects is described in OCA Secretary and Author, Bob's book, "Astronomical Discoveries You Can Make, Too! - Replicating the work of the great observers".

So on to the images and data analysis.  I planned to take a week's worth of observations and plot the observed positions of the moons.  As luck goes though, we amateurs know that things come up, like the weather clouding out some nights, so I have some missing nights of observations.

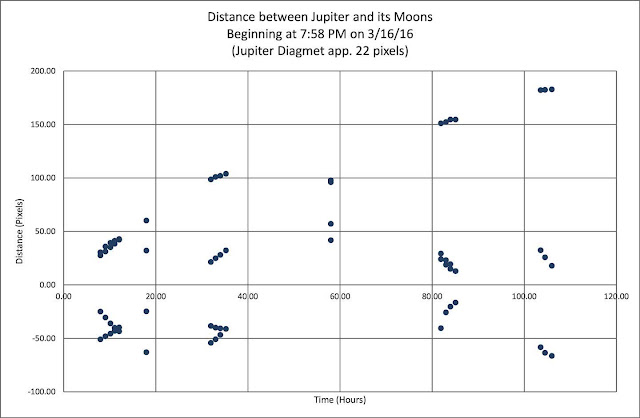
The first image is a plot of the distance (in pixels) between the observed moons and Jupiter. 

Measured positions of Jupiter's Moons (Source: Palmia Observatory)

The vertical axis is the distance in pixels from my camera with a 300 mm telephoto lens.  The horizontal axis is the time in hours.  Can you see any pattern in the data?  The moons positions should trace out a sinusoidal curve.  Can you start to make out the pattern?  Mostly all four moons are visible, but sometimes a moon is missing because it is hidden by Jupiter.

The second attached photo shows my eyeball data fitting using the known orbital periods. 

Fitting four curves through the observed points for the four moons of Jupiter (Source: Palmia Observatory)

Note there that I can actually identify which moon is which because I can build on the knowledge of other scientist over the course of hundreds of years.  I just used the known periods and semi majors axes of the moon to curve fit sinusoids and didn't rely on any least squares algorithm or gravity type orbit calculations.  Doing the real orbit calculations is much more complicated and will probably take me a couple of weeks.

Finally, you might be wondering what the raw data observation looks like.  The third attached photo shows the raw image typical for Jupiter taken with just my DSLR and 300 mm lens. 

Using AP4WIN to analyze the positions of Jupiter's Moons (Source: Palmia Observatory)

My amateur learning curve is to select the exposure setting so that I don't overexpose and blur the image or underexpose and not be able to detect any background stars.  For the plots presented this week background stars are not necessary.  Exposure times were set between 1/30 to 2 seconds, with 1/2 second used for the distance measurements.

So stay tuned for next week's review of the harder orbit calculation and progress.

Until next time,
Resident Astronomer George

There are over 200 postings of similar topics on this blog

If you are interested in things astronomical or in astrophysics and cosmology

Check out this blog at www.palmiaobservatory.com